This page has a set of practice questions that cover most topics in COMP2521 23T3 and will give you a chance to test your knowledge of data structures and algorithms.
Note that the theory questions in the real COMP2521 23T3 exam will not be multiple choice!
Question 1 - Minimum Spanning Tree
Given this graph, find the total weight of the minimum spanning tree.
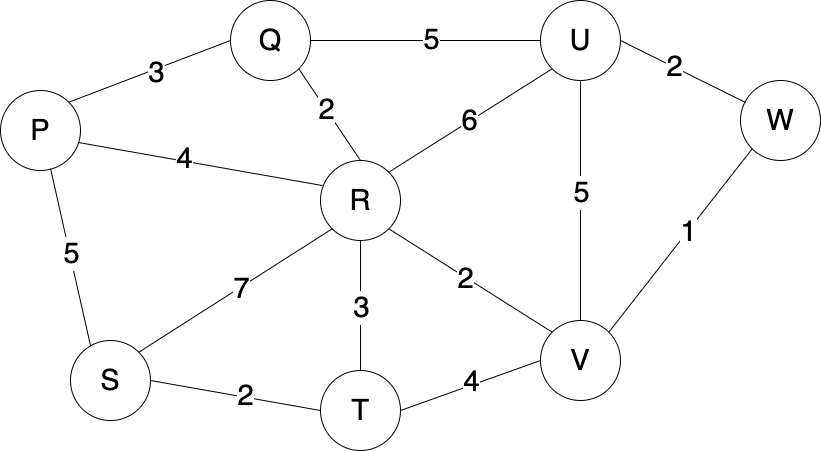
14
15
16
18
Question 2 - Graph Traversal Algorithms
Consider the following iterative functions for breadth-first and depth-first traversal on a graph.
Show what would be printed by the following calls to these functions on this graph.
When visiting neighbouring vertices, assume they are visited in ascending order.
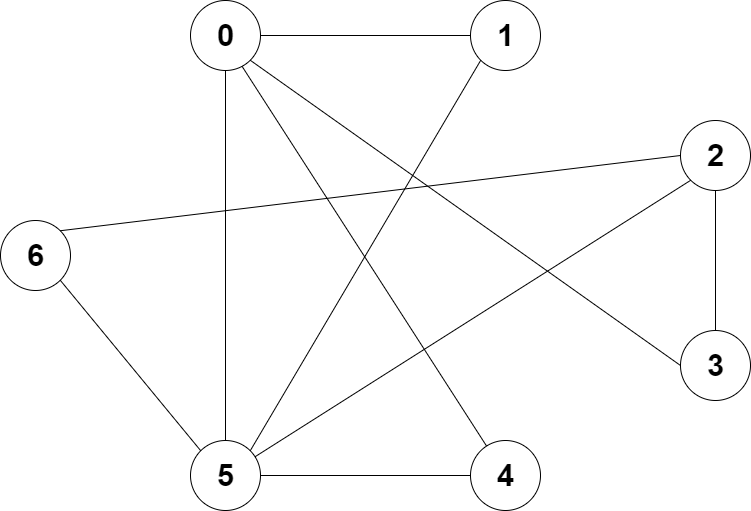
a) breadthFirst(g, 3)
b) depthFirst(g, 0)
a) 3, 2, 0, 6, 5, 4, 1
b) 0, 1, 5, 2, 3, 4, 6
a) 3, 0, 2, 1, 4, 5, 6
b) 0, 1, 5, 2, 3, 6, 4
a) 3, 0, 1, 5, 2, 6, 4
b) 0, 1, 5, 4, 2, 3, 6
a) 0, 1, 5, 2, 4, 6, 3
b) 3, 0, 1, 5, 2, 6, 4
Question 3 - Time complexity
Find the Big-O time complexity of the following function in terms of n where n is the number of elements in the nums array.
void print_nums(int nums[]) {
for (int i = 0; i < 100; i++) {
printf(""%d\n"", nums[i]);
}
}
O(1)
O(100)
O(n)
O(n ^ 2)
Question 4 - Euler paths
Does an Euler path/circuit exist for this graph?
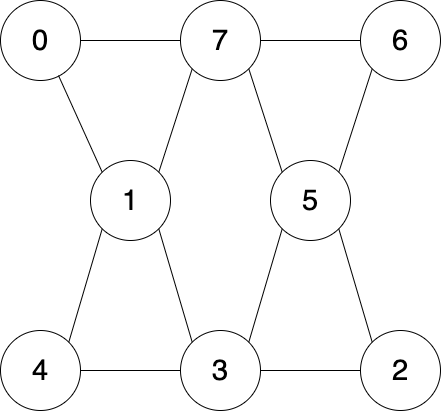
Has Euler path, has Euler circuit
Has Euler path, has no Euler circuit
Has no Euler path, has Euler circuit
Has no Euler path, has no Euler circuit
Question 5 - Sorting
In which of the following sorting algorithms is the performance for both sorted and reverse inputs slower than random inputs?
Bubble sort
Selection sort
Naive quicksort
Merge sort
Question 6 - Time complexity
Find the time complexity of this function in Big-O notation in terms of n.
# Assume n is the size of the dynamically allocated array `arr`
int function(int n, int* arr) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < i; j++) {
arr[i] += 1;
}
}
int total = 0;
for (int i = 0; i < n; i++) {
total += arr[i];
}
return total;
}
O(n)
O(n^2)
O(n^2 + n)
O(n log(n))
Question 7 - Time complexity
Find the time complexity of this function in Big-O notation in terms of n.
# Assume n >= 0
void halve(int n) {
if (n == 0) {
return;
}
halve(n / 2);
}
O(1)
O(log(n))
O(n)
O(2 ^ n)
Question 8 - Time complexity
Find the time complexity of this function in Big-O notation in terms of n and m.
# Assume n > m > 0
int rem(int n, int m) {
while (n >= m) {
n -= m;
}
return n;
}
O(n + m)
O(n - m)
O(n * m)
O(n / m)
Question 9 - AVL Trees
After inserting 45 into this AVL tree, what will the tree look like?
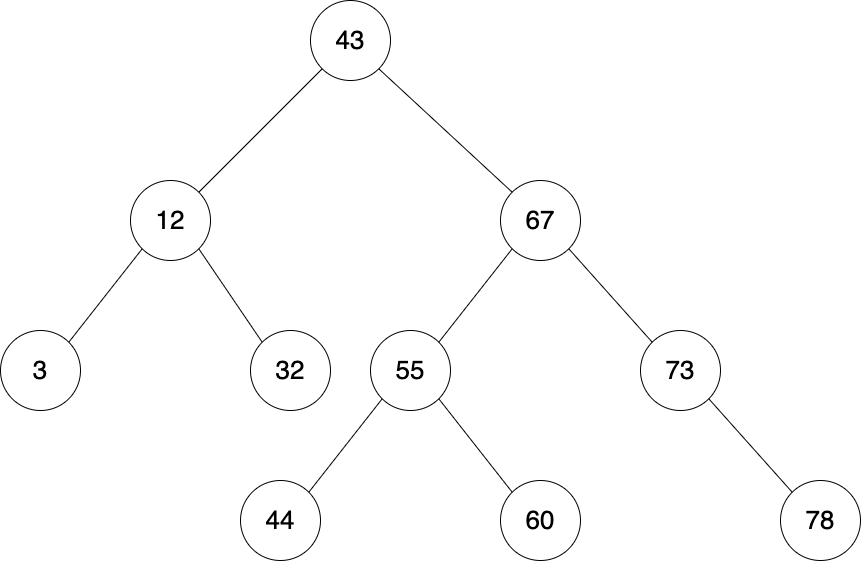
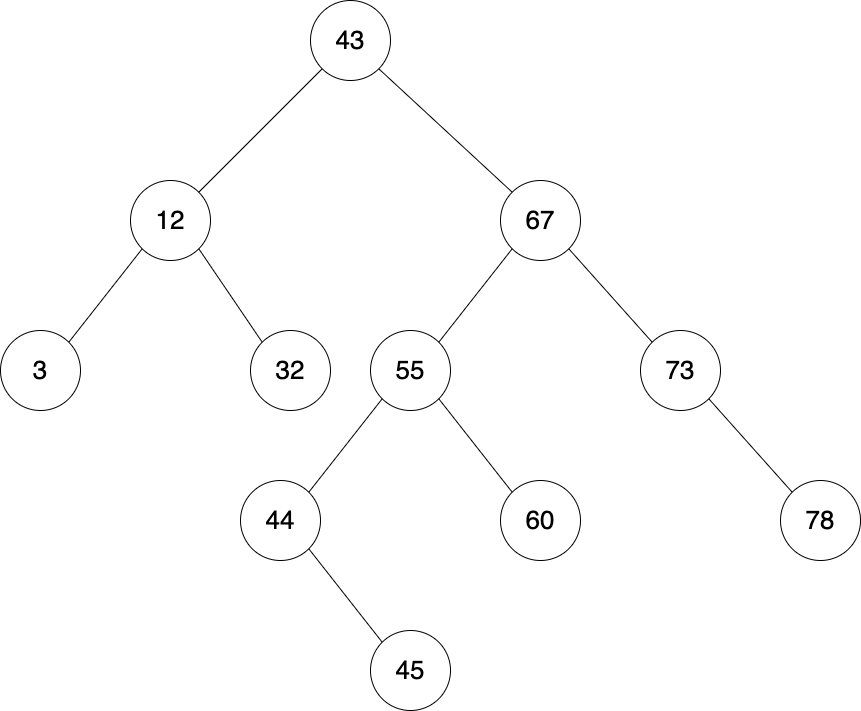
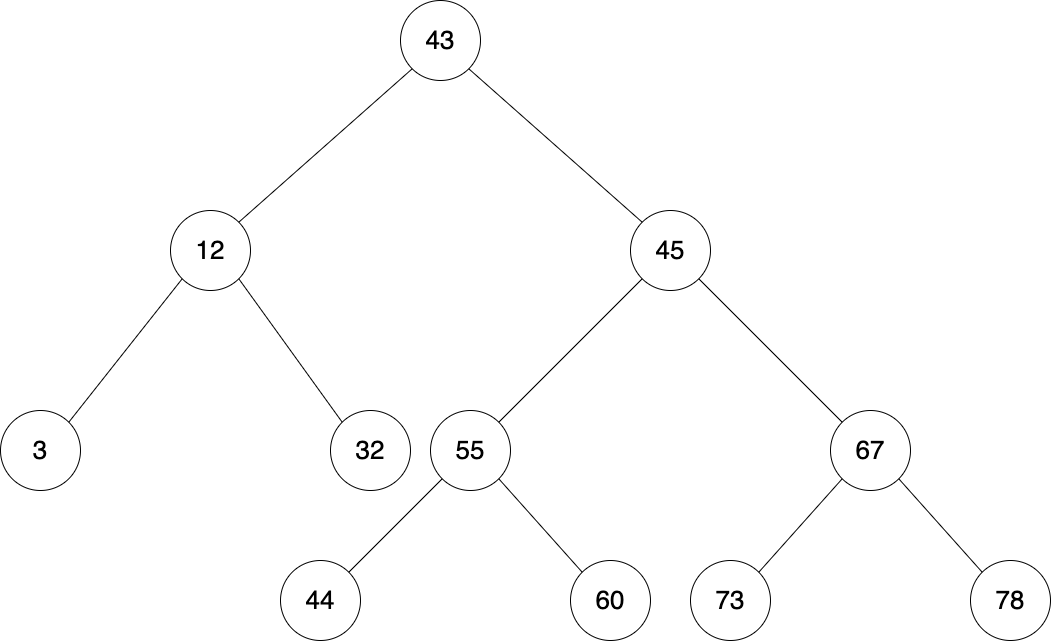

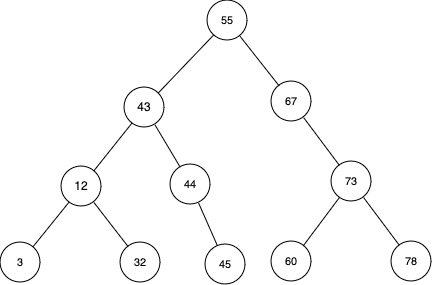
Question 10 - BFS and DFS
What is the difference between the implementation of iterative BFS and iterative DFS and the theoretical difference between the two?
BFS uses a queue, checking all neighbours of a node before moving on to another node, and DFS uses a stack, checking every new node as it is found.
BFS uses a stack, checking all neighbours of a node before moving on to another node, and DFS uses a queue, checking every new node as it is found.
BFS uses a queue, checking every new node as it is found, and DFS uses a stack, checking all neighbours of a node before moving on to another node.
BFS uses a stack, checking every new node as it is found, and DFS uses a queue, checking all neighbours of a node before moving on to another node.
Question 11 - Graph ordering
Which of the following is post order?
-
Traverse the left subtree, i.e., call recursion (left-subtree).
-
Visit the root (i.e., do work on the current node).
-
Traverse the right subtree, i.e., call recursion (right-subtree).
-
Visit the root (i.e., do work on the current node).
-
Traverse the left subtree, i.e., call recursion (left-subtree).
-
Traverse the right subtree, i.e., call recursion (right-subtree).
-
Traverse the left subtree, i.e., call recursion (left-subtree).
-
Traverse the right subtree, i.e., call recursion (right-subtree).
-
Visit the root (i.e., do work on the current node).
None of the above.
Question 12 - Tree Rotations
What sequence of rotations will transform this tree to end up with 7 at the root?
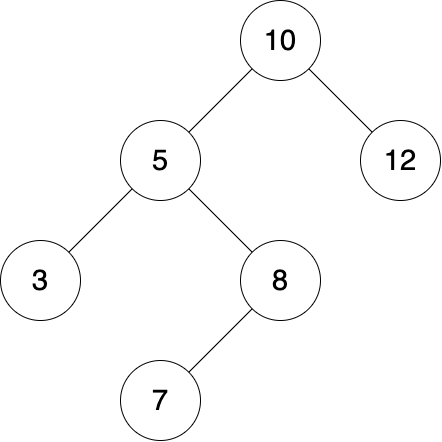
rotate_right(7), rotate_left(8), rotate_right(5)
rotate_left(8), rotate_right(5), rotate_left(10)
rotate_left(5), rotate_right(8), rotate_right(8)
rotate_right(8), rotate_left(5), rotate_right(10)
Question 13 - Kruskal's Algorithm
Using Kruskal's algorithm, find the minimum spanning tree of this fully connected and weighted graph.
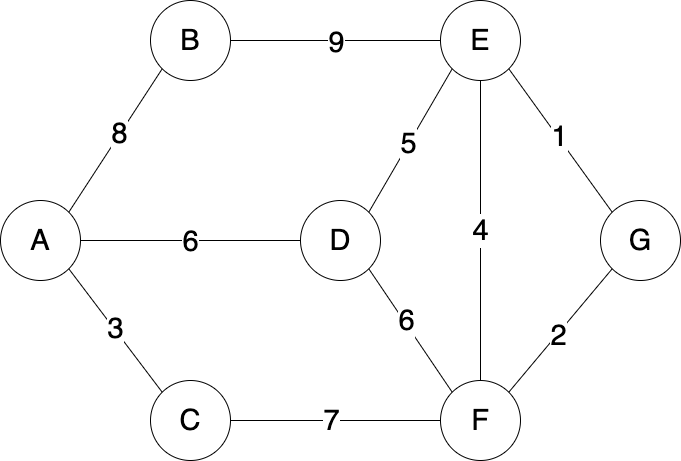
During this procedure, how many times do you encounter a cycle before you find the MST?
0
1
2
3
Question 14 - Tree Rotations
Which sequence of transformations will make the following transformation?
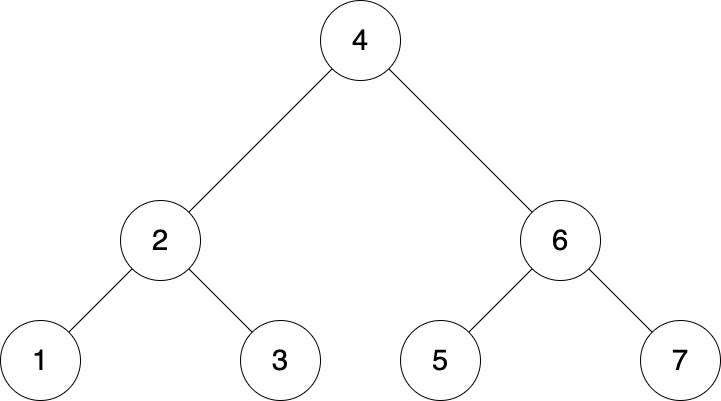
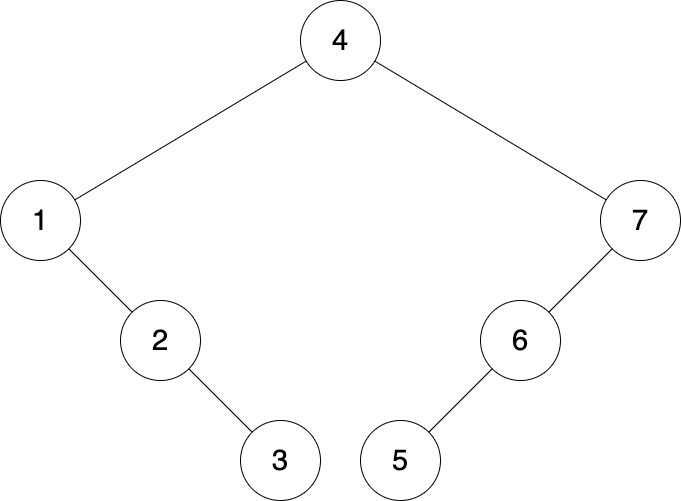
rotate_right(1), rotate_left(7)
rotate_right(2), rotate_left(6)
rotate_right(5), rotate_left(3)
rotate_right(6), rotate_left(2)
Question 15 - Dijkstra's Algorithm (Challenge)
Using Dijkstra's algorithm, find the shortest path from A to all other vertices in this fully connected directed and weighted graph.
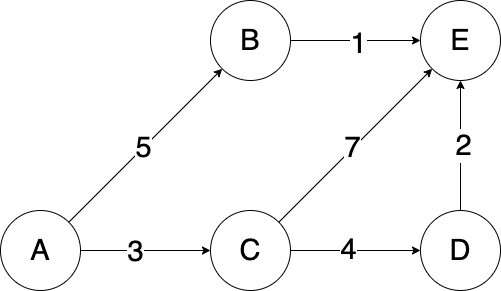
During this procedure, how many times is an edge relaxed towards vertex E? In other words, on how many occasions do we update our knowledge of the shortest distance from A to E?
0
1
2
3
Question 16 - Time complexity (Challenge)
What is the time complexity of the following function?
# Assume n > 0
void print_pairs(int n) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j += i) {
printf("%d %d\n", i, j);
}
}
}
O(n)
O(n * log(n))
O(n^1.5)
O(n^2)
Good luck for the exam! Remember; you've been preparing for it for the entire term so all that's left is to apply everything you've learned and to do your best :D